Classical Momentum and Nesterov’s Accelerated Gradient Descent

31 Jul 2015

冲量（Classical Momentum， 简写为 CM ）和 Nesterov 加速 （ Nesterov’s Accelerated Gradient (NAG) ） 在 SGD 中常用，他们的步骤相似。经典的冲量表示如下：

\[\begin{align} \Delta \theta_t &= \alpha \Delta \theta_{t-1} - \eta \nabla f(\theta_{t-1}) \\ \theta_t &= \theta_{t-1} + \Delta \theta_t \end{align}\]

Nesterov’s Accelerated Gradient (NAG) 的方法表示如下 [1]

\[\begin{align} y_{s+1} &= x_s - \eta \nabla f(x_s) \\ x_{s+1} &= (1+\alpha)y_{s+1} - \alpha y_s \end{align}\]

其中 \(\eta\) 是步长，在 NAG 中 \(\eta = 1/\beta\)， \(\alpha = \frac{\sqrt{Q}-1}{\sqrt{Q}+1}\)， \(Q\) 是函数的条件数。NAG 的理解比较困难，Sébastien Bubeck 提供了一个从几何角度的解释 [2]。其实 NAG 可以表示为经典的冲量类似的形式 [3]。

我们定义 \(\theta_s = y_s\)， 以及 \(\Delta \theta_{s+1} = \theta_{s+1} - \theta_s\)， 从 NAG 的 \(x_s\) 的 updating rule 可以得到

\[\begin{align} x_{s+1} &= (1+\alpha) \theta_{s+1} - \alpha \theta_s \\ &= \theta_{s+1} + \alpha (\theta_{s+1} - \theta_s) \\ &= \theta_{s+1} + \alpha \Delta \theta_{s+1} \end{align}\]

因此有 \(x_{s} = \theta_{s} + \alpha \Delta \theta_{s}\)， 代入 NAG 的 \(y_{s+1}\) 迭代公式可以得到

\[\begin{align} \theta_{s+1} &= \theta_{s} + \alpha \Delta \theta_{s} - \eta \Delta f(\theta_{s} + \alpha \Delta \theta_{s}) \\ \Rightarrow \ \Delta \theta_{s+1} &= \alpha \Delta \theta_{s} - \eta \Delta f(\theta_{s} + \alpha \Delta \theta_{s}) \end{align}\]

因此 NAG 可以看作如下的更新过程

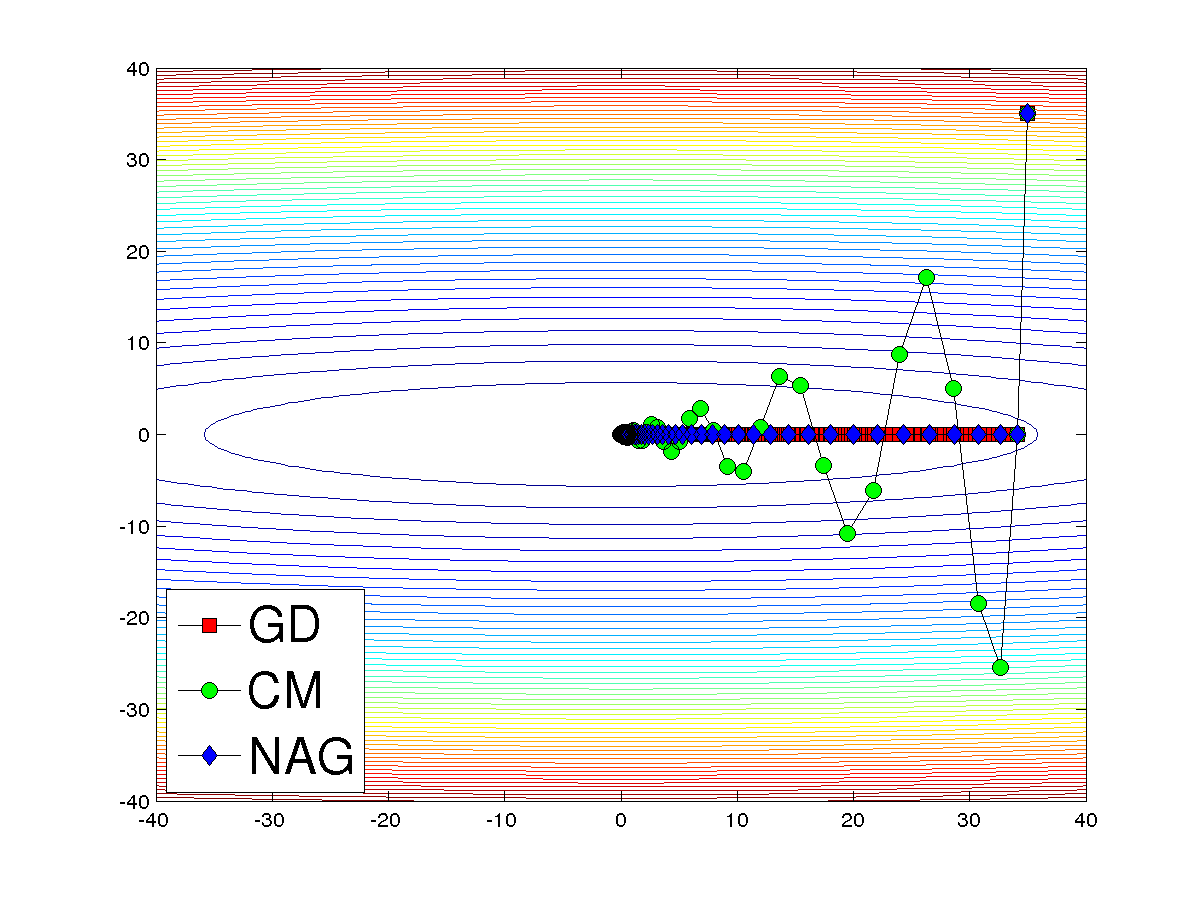
\[\begin{align} \Delta \theta_{s+1} &= \alpha \Delta \theta_{s} - \eta \Delta f(\theta_{s} + \alpha \Delta \theta_{s}) \\ \theta_{s+1} &= \theta_s + \Delta \theta_{s+1} \end{align}\]

和 CM 对比可以看出， 他们的区别仅仅在于求梯度的步骤， NAG 的梯度要比 CM 要提前一步。如果步长合适， NAG 比 CM 有优势，如果不合适就情况就不一定了。下图中用的步长是对于 NAG 在理想情况下的步长。代码见这里。从图中可以看出 NAG 确实比 CM 更稳定一点。其实如果步长选的不合适，有些情况下 CM 可能会比 NAG 稳定， 因为在求梯度的时候 NAG 比 CM 更激进一点。

Reference

1. Bubeck, Sébastien. “Theory of convex optimization for machine learning.” arXiv preprint arXiv:1405.4980 (2014).
2. Revisiting Nesterov’s Acceleration
3. Sutskever, Ilya, et al. “On the importance of initialization and momentum in deep learning.” Proceedings of the 30th international conference on machine learning (ICML-13). 2013.