How to escape from saddle points?
10 Sep 2015在神经网络尤其是深度神经网络中,鞍点的数量比局部最小值的数量要多很多。鞍点会让 gradient descent 收敛更慢(鞍点附近的梯度太小),甚至会收敛到鞍点。因此如何利用二阶信息来逃离鞍点有必要。然而针对凸问题而设计的牛顿法并不适合这样的场景。牛顿法会被鞍点吸引,牛顿方向甚至不是下降方向,因此不适合 deep learning 的优化。普通的 gradient descent 都会比牛顿法要好。一个比较容易想到的方法是把 Hessian matrix 的负特征值给删掉,仅仅保留正的特征值,但是这种方法不能利用负特征值对应的特征向量的方向。在负的特征值的特征向量对应的下降的方向有可能是下降很快的方向(对于任意的特征向量 \(q\), \(-q\) 也是特征向量,和梯度的内积为负的那个才是下降的方向)。我们的问题是有没有更好的、所有特征向量都能用上的方法。在[2]中作者提出用 absolute Hessian matrix 作为 preconditioning matrix,absolute Hessian matrix 的定义为
\[|H| = \sum_i |\lambda_i| q_iq_i^T\]其中 \(\lambda_i\) 和 \(q_i\) 是 Hessian matrix 对应的特征值和特征向量(这种方法不是[2]第一个提出来的)。它的目的是为了使 precondition 之后的 Hessian matrix 的条件数为1。这可能是非凸问题非常好的局部下降方向,但是没有找到证明。这个方法有个直观的理解: \(H\) 是 梯度的变化率,那么 \(H=I\) 说明在局部梯度 \(g\) 仅仅在对应的坐标上有变化(而且变化相同),这样可以用较大的步长(一般需要line search),如果存在一个线性变换使得变换后的函数的 Hessian matrix 为 \(I\),那么可以在变换后的梯度上用较大的步长(每个component的步长相同),这样的梯度更新等价于在原先的坐标中对梯度应用 preconditioner。这个论述对于凸问题是显然成立的,对于非凸问题其实同样也成立,因为仅仅考虑了 \(f\) 和 \(g\) 的变化率,并没有考虑别的因素。因此对于非凸问题,这个迭代方式很可能是最优的
\[\theta = \theta - \eta |H|^{-1} \nabla f(\theta)\]我们可以在一个 toy 函数上验证 absolute Hessian matrix 的行为。下图是函数 \(f(x) = x^THx\) (\(H\) 不是正定的)上各种方法的轨迹。可以看出:1)牛顿方向不一定是下降方向,2)牛顿法可以被 saddle points 吸引,3)absolute Hessian matrix 对应的方向有逃离鞍点的作用。因此 absolute Hessian matrix 是个很好的选择。图的代码见这里。
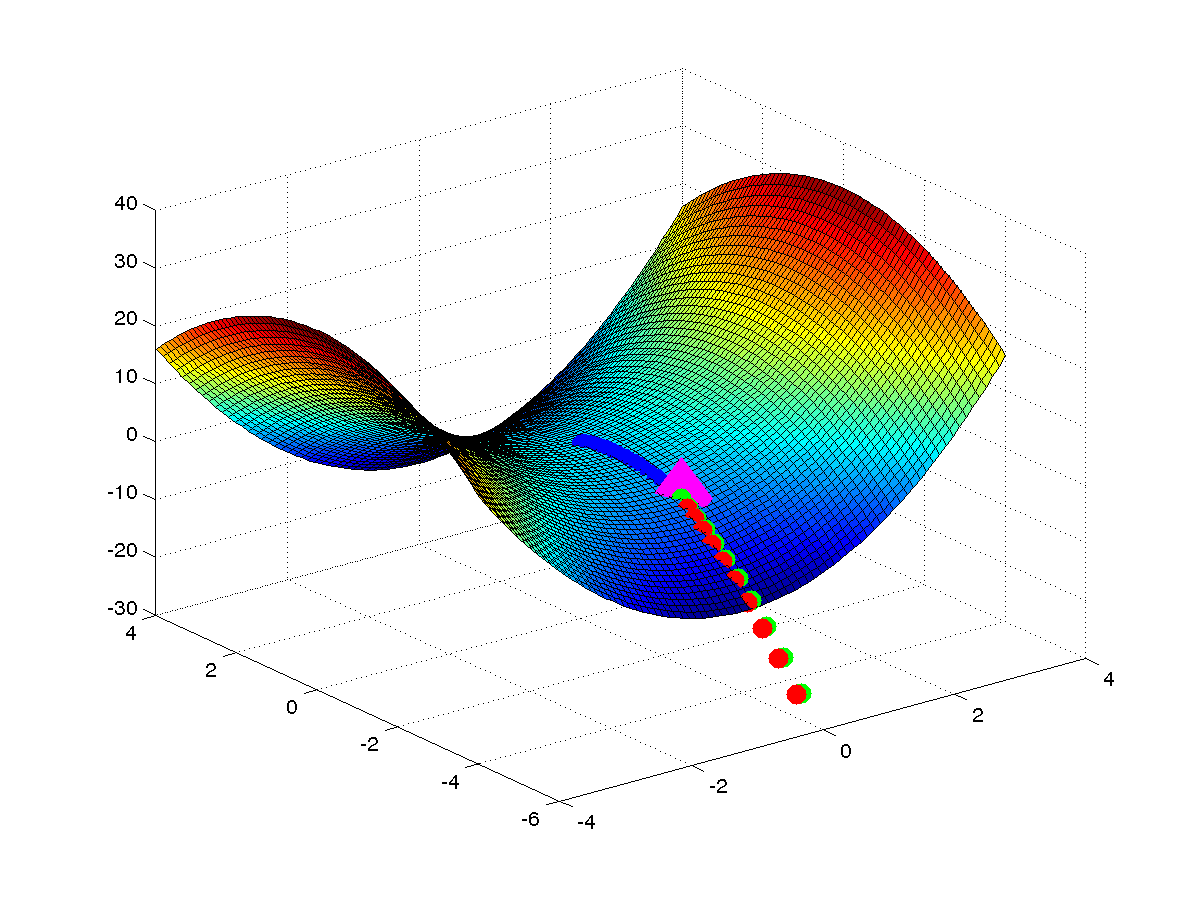
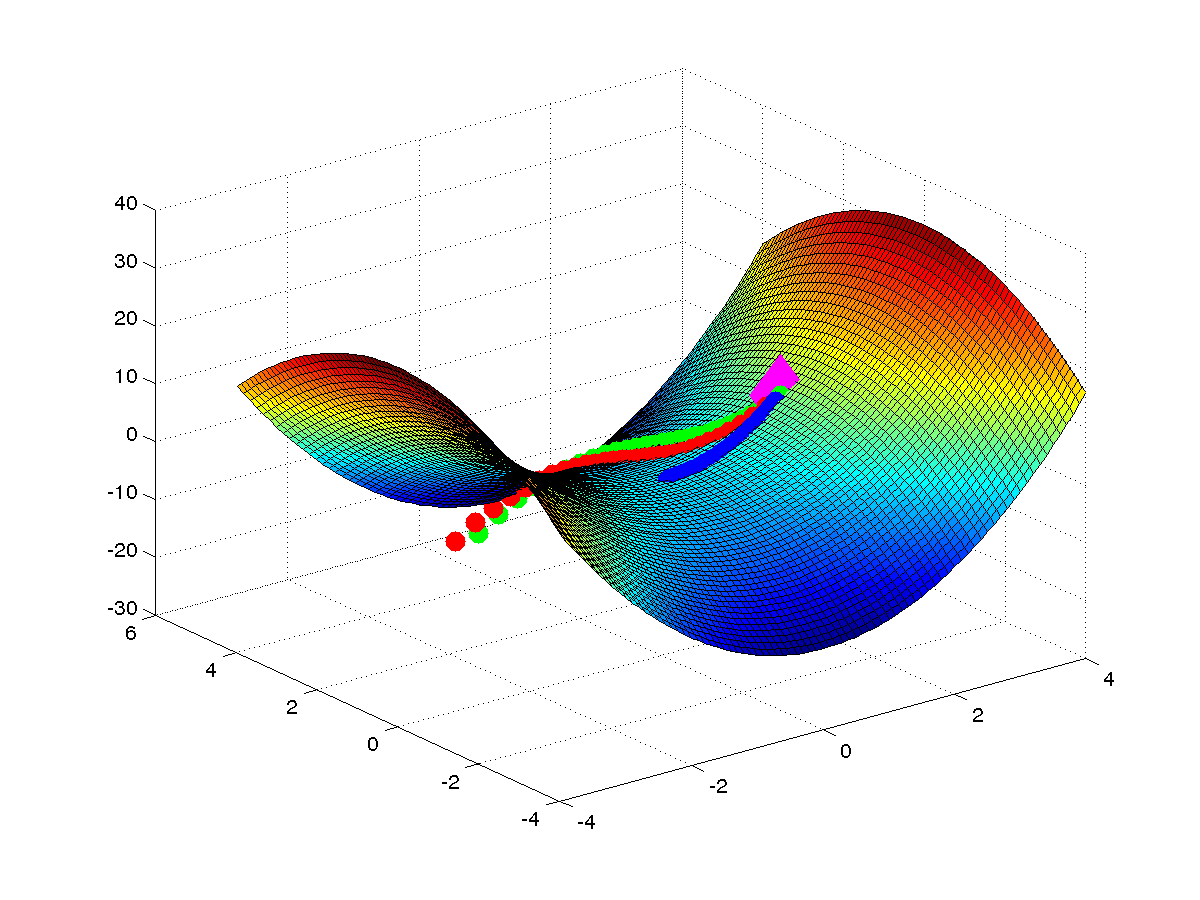
由于计算 absolute Hessian matrix 的复杂度太大,我们仅仅考虑其对角线来近似,同样的近似方法也被用来近似 Hessian matrix([2]中没有给出近似程度的好坏的证明)。因此我们的目标本来是找
\[D^{-1} = |H|^{-1}\]但是不好算,因此我们考虑用对角阵
\[D = diag(|H|) = diag(\sqrt{H^2})\]这个同样不好算。因此[2]中用(\(H^2\)的对角线)
\[D = diag(|H|) \approx \sqrt{diag(H^2)}\]来近似。这个近似要比 (\(H\)的对角线)
\[D = diag(|H|) \approx \sqrt{diag(H)^2} = |diag(H)|\]要好一点(这个又叫做 Jacobi preconditioner)。\(\sqrt{diag(H^2)}\)的对角线的元素其实就是 \(H\) 的行向量的模,这就是 [2] 的 title 中 equilibrated 的来源,这个preconditoiner 的本质是对 Hessian matrix 做了个“归一化”。\(H\) 的行向量的模仍然不好算,因此[2] 中用 \(D = \sqrt{E[(Hv)^2]}\) 来近似,其中 \(v\) 是一个高斯分布的随机向量。在 Theano 中可以用 R-operator 来求 \(Hv\)。用这个理论可以部分地解释 Hinton 的 RMSprop。
Reference
- Yann Dauphin, Razvan Pascanu, Caglar Gulcehre, Kyunghyun Cho, Surya Ganguli, Yoshua Bengio. “Identifying and attacking the saddle point problem in high-dimensional non-convex optimization.” Advances in Neural Information Processing Systems. 2014.
- Yann N. Dauphin, Harm de Vries, Yoshua Bengio. “Equilibrated adaptive learning rates for non-convex optimization.” Advances in Neural Information Processing Systems. 2015